Teorema de Rouché-Frobenius
Sea el sistema con ecuaciones lineales sobre un cuerpo y con incógnitas, siendo y naturales mayores que 0. Entonces,
- El sistema es compatible si, y sólo si, rango(A) = rango(A|b)
- El sistema es compatible determinado si, y sólo si, rango(A) = rango(A|b)= n.
Demostracion
Representamos por a la matriz en forma escalonada reducida de .
Existe una matriz regular tal que . Esta matriz es la matriz producto de las matrices elementales que nos permiten obtener la forma escalonada reducida de .
Como la matriz es regular, el sistema es equivalente a .
Como el sistema tiene forma escalonada reducida, se le puede aplicar el método de Gauss-Jordan y se tiene que:
es compatible si y sólo si lo es, y esto es equivalente a que la última columna de la matriz no sea principal y, por tanto, a que
Pero de la definición de rango, de que y de la igualdad anterior, tenemos que
Así, queda demostrado el primer apartado.
Del mismo modo, el sistema es determinado si y sólo si también lo es.
Esto es lo mismo que decir que en la matriz , todas las columnas son principales excepto la última. Esto equivale a su vez a que
De donde se obtiene
b
ejemplos
Ejemplo 1
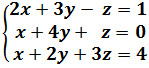
La matriz ampliada del sistema es:
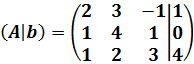
El rango de la matriz anterior es 3 puesto que el determinante de es no nulo:
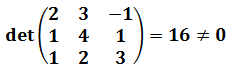
Por tanto, tenemos que los rangos de las dos matrices, y , coinciden:
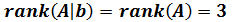
Por el teorema de Rouché-Frobenius, como los rangos son iguales y coinciden con el número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
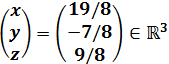
Es decir,
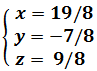
Ejemplo 2
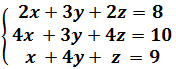
La matriz ampliada del sistema es
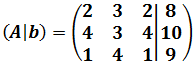
Mediante operaciones elementales fila, obtenemos que la matriz forma escalonada reducida (FER) equivalente a la matriz anterior es
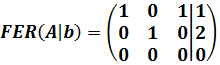
De la forma de la matriz deducimos que los rangos de las matrices ampliada y coeficientes coinciden y es 2, aunque es menor que el número de incógnitas:
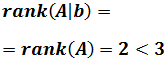
Por el teorema de Rouché-Frobenius, como los rangos coinciden pero son menores que el número de incógnitas, el sistema es compatible indeterminado.
De la propia obtenemos el conjunto de soluciones del sistema:
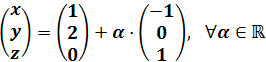
Es decir,
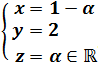

No hay comentarios:
Publicar un comentario