Un sistema de ecuaciones lineales tiene infinitas soluciones cuando las ecuaciones son dependientes, es decir, una ecuación se puede obtener a partir de otra mediante multiplicación por un escalar o combinación lineal. Esto suele ocurrir en sistemas con menos ecuaciones que incógnitas o cuando las ecuaciones representan la misma recta en un espacio bidimensional.
Sistemas de ecuaciones -mate IV
sábado, 1 de febrero de 2025
Aplicaciones Economicas
Los sistemas de ecuaciones lineales son una herramienta fundamental en la economía, ya que permiten modelar y analizar diversas situaciones económicas. Algunas de sus aplicaciones más comunes son:
-
Análisis de equilibrio de mercado: Los sistemas de ecuaciones lineales se utilizan para encontrar el punto de equilibrio en un mercado, donde la oferta y la demanda se igualan. Esto permite determinar el precio y la cantidad de equilibrio de un producto o servicio.
-
Optimización de recursos: Las empresas utilizan sistemas de ecuaciones lineales para optimizar la asignación de sus recursos, como la producción, la mano de obra y el capital. Esto les permite maximizar sus ganancias o minimizar sus costos.
-
Análisis de insumo-producto: Los sistemas de ecuaciones lineales se utilizan para analizar las relaciones entre los diferentes sectores de una economía. Esto permite determinar cómo los cambios en un sector afectan a otros sectores y a la economía en su conjunto.
-
Modelos econométricos: Los sistemas de ecuaciones lineales son la base de muchos modelos econométricos, que se utilizan para pronosticar variables económicas y evaluar el impacto de políticas económicas.
-
Toma de decisiones: Los sistemas de ecuaciones lineales pueden ayudar a las empresas y a los gobiernos a tomar decisiones informadas sobre precios, producción, inversión y otras variables económicas.
En resumen, los sistemas de ecuaciones lineales son una herramienta esencial para el análisis económico y la toma de decisiones en una amplia variedad de contextos.
Sistema de ecuaciones lineales. Método de la inversa
El método de la matriz inversa se basa en la forma matricial de un sistema de ecuaciones lineales, que es:
AX = BDonde:
• A es la matriz de coeficientes.
• X es la matriz columna de variables (las incógnitas).
• B es la matriz columna de términos independientes.
Si la matriz de coeficientes A es invertible (es decir, si existe su matriz inversa, A⁻¹), entonces podemos encontrar la solución del sistema de la siguiente manera:
1. Multiplicamos ambos lados de la ecuación
AX = B por la izquierda por A⁻¹:A⁻¹(AX) = A⁻¹B2. Usamos la propiedad asociativa de la multiplicación de matrices:
(A⁻¹A)X = A⁻¹B3. Dado que A⁻¹A es igual a la matriz identidad I, tenemos:
IX = A⁻¹B4. Dado que la matriz identidad no modifica a una matriz cuando multiplica a otra, obtenemos la solución:
X = A⁻¹BPor lo tanto, para resolver un sistema de ecuaciones lineales usando el método de la inversa, necesitamos:
1. Calcular la inversa de la matriz de coeficientes A (si es que existe).
2. Multiplicar la inversa A⁻¹ por la matriz de términos independientes B. El resultado será la matriz X, que contiene los valores de las variables.
1. Verificar que la matriz A sea invertible:
• Calcula el determinante de la matriz A (det(A)).
• Si det(A) ≠ 0, entonces la matriz A es invertible y se puede usar el método de la inversa. Si det(A) = 0, el método de la inversa no se puede aplicar.
2. Calcular la matriz inversa (A⁻¹):
• Hay varias formas de calcular la inversa. Los métodos más comunes son:
* Método de la Matriz Aumentada (Gauss-Jordan): Se crea una matriz aumentada [A | I] y se aplican operaciones elementales de fila hasta que A se convierta en la matriz identidad. La parte que estaba originalmente en la identidad se convierte en la inversa de A.
* Método de la Matriz Adjunta: Se calcula la matriz de cofactores, se transpone para obtener la matriz adjunta, y luego se divide por el determinante de A. Este método es adecuado para matrices pequeñas (2x2 y 3x3).
* Existen herramientas computacionales (como Matlab, Octave, NumPy en Python, etc.) que permiten calcular la matriz inversa de forma rápida y sencilla.
3. Multiplicar A⁻¹ por B:
• Una vez que tienes la matriz inversa (A⁻¹), se realiza la multiplicación de matrices A⁻¹B.
• El resultado de esta multiplicación es la matriz X, que contiene las soluciones para cada variable del sistema.
Teorema de Rouché-Frobenius
Teorema de Rouché-Frobenius
Sea el sistema Ax=b con m ecuaciones lineales sobre un cuerpo K y con n incógnitas, siendo m y n naturales mayores que 0. Entonces,
- El sistema Ax=b es compatible si, y sólo si, rango(A) = rango(A|b)
- El sistema Ax=b es compatible determinado si, y sólo si, rango(A) = rango(A|b)= n.
Demostracion
Representamos por FER(A) a la matriz en forma escalonada reducida de A.
Existe una matriz regular P tal que FER(A)=PA. Esta matriz P es la matriz producto de las matrices elementales que nos permiten obtener la forma escalonada reducida de A.
Como la matriz P es regular, el sistema (PA)x=FER(A)x=Pb es equivalente a Ax=b.
Como el sistema FER(A)x=Pb tiene forma escalonada reducida, se le puede aplicar el método de Gauss-Jordan y se tiene que:
Ax=b es compatible si y sólo si FER(A)x=Pb lo es, y esto es equivalente a que la última columna de la matriz [FER(A)|Pb] no sea principal y, por tanto, a que
rango(FER(A)|Pb)=rango(FER(A))
Pero de la definición de rango, de que FER(A|b)=[FER(A)|Pb] y de la igualdad anterior, tenemos que
rango(A|b)=rango(FER(A))=rango(A)
Así, queda demostrado el primer apartado.
Del mismo modo, el sistema Ax=b es determinado si y sólo si FER(A)=Pb también lo es.
Esto es lo mismo que decir que en la matriz FER(A|Pb), todas las columnas son principales excepto la última. Esto equivale a su vez a que
rango(FER(A)|Pb)=rango(FER(A))=n
De donde se obtiene
rango(A)=n=rango(A|
b
ejemplos
Ejemplo 1
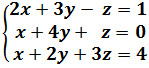
La matriz ampliada del sistema es:
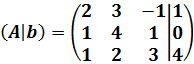
El rango de la matriz anterior es 3 puesto que el determinante de A es no nulo:
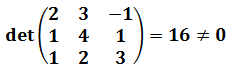
Por tanto, tenemos que los rangos de las dos matrices, A y (A|b), coinciden:
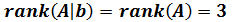
Por el teorema de Rouché-Frobenius, como los rangos son iguales y coinciden con el número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
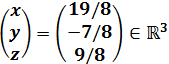
Es decir,
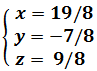
Ejemplo 2
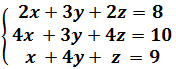
La matriz ampliada del sistema es
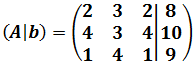
Mediante operaciones elementales fila, obtenemos que la matriz forma escalonada reducida (FER) equivalente a la matriz anterior es
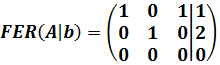
De la forma de la matriz deducimos que los rangos de las matrices ampliada y coeficientes coinciden y es 2, aunque es menor que el número de incógnitas:
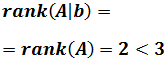
Por el teorema de Rouché-Frobenius, como los rangos coinciden pero son menores que el número de incógnitas, el sistema es compatible indeterminado.
De la propia FER(A|b) obtenemos el conjunto de soluciones del sistema:
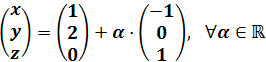
Es decir,
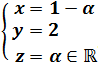
Sistema de ecuaciones lineales con infinitas soluciones
Un sistema de ecuaciones lineales tiene infinitas soluciones cuando las ecuaciones son dependientes, es decir, una ecuación se puede obten...
-
El método de la matriz inversa se basa en la forma matricial de un sistema de ecuaciones lineales, que es: AX = B Donde: • A es la matri...
-
Un sistema de ecuaciones lineales tiene infinitas soluciones cuando las ecuaciones son dependientes, es decir, una ecuación se puede obten...
-
Idea Central del Método de Gauss-Jordan: El método de Gauss-Jordan se basa en la aplicación de *operaciones elementales de fila* a la matr...

